The quality of a dataset plays a fundamental role in the success of any machine learning project. Poor data quality can significantly hinder the model’s ability to learn meaningful patterns, leading to unreliable predictions, biased outcomes, and reduced generalisability.

Missing data poses as one of the most common data quality issues. Missing data can lead to biased models if not handled properly. This article contains various subsections as given below:

• Reasons for Missing Values in Datasets
• Understanding the types of Missing Data (MCAR, MNAR, and MAR)
• How to Identify the Type of Missing Data

---

Reason for Missing Values in Datasets

1. Data Collection Issues:

• Surveys and questionnaires may have skipped questions (affecting categorical and ordinal data).
• Sensors and devices may fail to record measurements (affecting numerical data).

2. Human Factors:

• Sensitive questions like income or demographics are often left unanswered (affecting ratio and nominal data).
• Subjective questions like satisfaction ratings may be skipped (affecting ordinal data).

3. Technical Problems:

• Equipment malfunctions can result in missing continuous and interval data (e.g., weather sensors failing to record temperature).

4. Systematic Exclusions:

• Certain groups may systematically omit responses due to cultural or social factors (affecting all types of data).

---

Understanding the types of Missing Data

The missing data can be classified into three categories:

1. MCAR (Missing Completely at Random)
2. MAR (Missing at Random)
3. MNAR (Missing Not at Random)

Missing Completely at Random (MCAR)

MCAR occurs when the data missing does not depend on any values in the dataset (observed or missing) and is completely random. Here, the probability of missing is unrelated to the data itself.

Example: A computer glitch randomly deleting some entries in a weather dataset or failing to record some values. Here the reasons for the failure are unknown.

Missing at Random (MAR)

MAR occurs when the data missing depends on other measured variables but not to any missing data. Here, the cause of missing data is related to other measured variables. MAR is a broader version of MCAR.

Example: A weighing scale producing more missing values when placed on a soft surface compared to a hard surface. Here we know the surface type that causes the missingness.

Missing not at Random (MNAR)

MNAR occurs when the data missing is related to other unobserved data or unmeasured data. Here the data may be missing for reasons unknown to us or reasons that cannot be measured. This type of data can cause significant bias in the data distribution. MNAR is the most complex case.

Example: In a study, it was observed that people with higher incomes are less likely to record their incomes. Hence most of the missing income data came from people with higher income. This would cause a significant bias in the average income of the people as per the data observed.

---

How to Identify the Type of Missing Data

There are multiple ways to determine whether missing data in your dataset belongs to MCAR, MAR, or MNAR category.

1. Analyze Correlations Between Missingness

correlation — In the context of machine learning and data analysis, correlation refers to a statistical measure that quantifies the degree to which two variables are related. It indicates whether and how strongly pairs of variables are associated with each other.

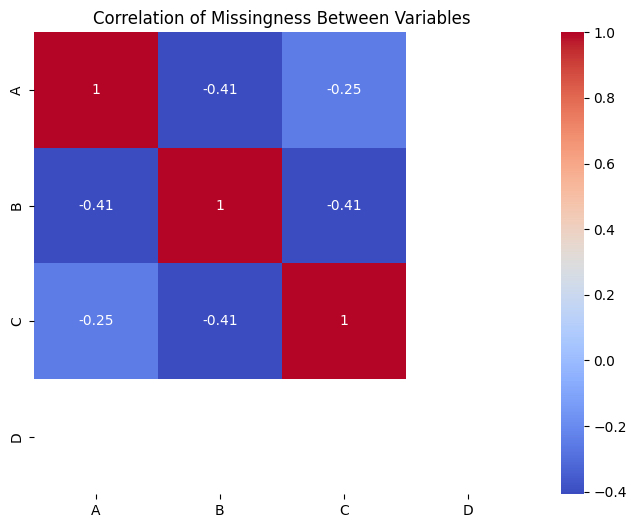
The heatmap in the provided image shows the correlation of missingness between variables. Here’s how to interpret it:

• MCAR — Low or Zero correlations in the heatmap suggest MCAR. If the missingness in one variable is not correlated with missingness or observed values in other variables, the data may be MCAR.
• MAR — Significant correlations in the heatmap suggest MAR. If the missingness in one variable is correlated with observed values of other variables, the data is likely to be MAR.
• MNAR — If missingness is related to the value of the variable itself (e.g., people with high incomes are less likely to report income), it is MNAR. This cannot be directly detected from correlations and requires domain knowledge.

2. Use Statistical Test

• For MCAR: Little’s MCAR test can be used to assess if the data is MCAR.

Little’s MCAR Test

A non significant p-value is used to indicate whether the data may be MCAR or not.

from scipy.stats import chi2

def little_mcar_test(data, alpha=0.05):
    """
    Performs Little's MCAR (Missing Completely At Random) test on a dataset with missing values.
    
    Parameters:
    data (DataFrame): A pandas DataFrame with n observations and p variables, where some values are missing.
    alpha (float): The significance level for the hypothesis test (default is 0.05).
    
    Returns:
    A tuple containing:
    - A matrix of missing values that represents the pattern of missingness in the dataset.
    - A p-value representing the significance of the MCAR test.
    """

    # Calculate the proportion of missing values in each variable
    p_m = data.isnull().mean()
    
    # Calculate the proportion of complete cases for each variable
    p_c = data.dropna().shape[0] / data.shape[0]
    
    # Calculate the correlation matrix for all pairs of variables that have complete cases
    R_c = data.dropna().corr()
    
    # Calculate the correlation matrix for all pairs of variables using all observations
    R_all = data.corr()
    
    # Calculate the difference between the two correlation matrices
    R_diff = R_all - R_c
    
    # Calculate the variance of the R_diff matrix
    V_Rdiff = np.var(R_diff, ddof=1)
    
    # Calculate the expected value of V_Rdiff under the null hypothesis that the missing data is MCAR
    E_Rdiff = (1 - p_c) / (1 - p_m).sum()
    
    # Calculate the test statistic
    T = np.trace(R_diff) / np.sqrt(V_Rdiff * E_Rdiff)
    
    # Calculate the degrees of freedom
    df = data.shape[1] * (data.shape[1] - 1) / 2
    
    # Calculate the p-value using a chi-squared distribution with df degrees of freedom and the test statistic T
    p_value = 1 - chi2.cdf(T ** 2, df)
    
    # Create a matrix of missing values that represents the pattern of missingness in the dataset
    missingness_matrix = data.isnull().astype(int)
    
    # Return the missingness matrix and the p-value
    return p_value

The function above returns p_value for each of the columns.

If p-value > 0.05 — The data is likely MCAR

If p-value ≤0.05 — The data is not MCAR (it could be MAR or MNAR)

3. Visualize Patterns

Create scatter plots with data points color-coded by missingness, box plots or histograms comparing distributions of observed vs. missing data for other variables.

• MCAR data should show even distribution of missingness
• MAR may show some patterns related to observed variables.
• MNAR will likely show clear patterns related to the missing variable itself.

 4. Use Domain Knowledge

Domain knowledge is critical for MNAR. It arises when missingness depends of unobserved values of the variable itself. This cannot be detected statistically but requires understanding of the dataset’s context.

By combining statistical tests, visualisations, and domain expertise, you can classify the type of missing data and make informed decisions for handling it effectively!

Thank you all for taking the time to read my article. The next article will be a detailed review of the different techniques that can be employed for handling the different types of missing data.